권찡's 공학이야기
푸리에 적분 본문
푸리에 급수와 주기함수에 대해서 알고 있어야 푸리에 적분을 이해하실수 있습니다.
이전 푸리에 급수를 다룰때 -L<x<L 구간에 대해서 정의된함수를 다뤘습니다.
푸리에 적분은 이 구간을 무한대로 확장하는 것으로 시작합니다.
이전에 푸리에 급수식은 아래와 같았습니다.


현재 우리가 사용하는 적분은 리만 적분이라는 것을 아실것입니다. 급수의 단위를 무한개로 쪼개고 합하는 형식의 적분을 말합니다.
고등학교에서도 적분을 처음 배울때 이렇게 배우기 시작하셨을 것입니다.
마찬가지로 푸리에 급수를 구간 확장을 통해서 적분으로 표현을 바꾼것이 퓨리에 적분입니다.
위의 푸리에 급수의 각 계수를 직접 푸리에 급수식에 대입해봅시다.

이때 각각의 삼각함수안의 값을 치환해줍시다. 보기 좋게

그리고 구간확장을 위해서 L을 무한대로 극한을 취해봅시다. 그로 인해 치환한 델타 뮤값은 0을 가지게 됩니다.

위의 치환과정과 극한을 거치고 나면 위 푸리에 급수는 아래와 같아 변하게 됩니다.

이것을 푸리에 적분이라고 하고, 내부의 적분식이 푸리에 계수를 나타내는 것이죠
구간확장을 통해서 푸리에 급수를 푸리에 적분으로 변환시키는 것입니다.
푸리에 계수만 다시 뽑아서 봅시다.

푸리에 급수와 마찬가지로 f(t)함수가 기함수일 경우 A=0, 우함수일경우 B=0 은 동일합니다.
푸리에 적분은 푸리에 급수를 우리가 고등학교때 배운것처럼 시그마를 극한을 취해서 적분으로 만드는 것과 사실상 동일합니다.
푸리에 급수에서 식으로 직접적으로 보여 드리진 않았지만 깁스 현상을 설명할때 썻던 함수를 푸리에 급수로 푸리에 적분으로 표현해봅시다.

이 식을 먼저 푸리에 급수로 표현해봅시다. 일단 위 함수가 기함수 형태를 띄고 있습니다. 따라서 A항에 관련된것은 모두 0의 값을 취합니다.
B항만 구하면 됩니다.

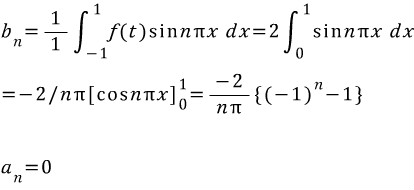

푸리에 급수는 위와 같이 구합니다. 마찬가지로 문제로 나온 기함수를 푸리에 적분식으로 변환하면



이런식으로 하는 것이 푸리에 적분으로 표현한 식입니다.
본함수가 단위계단 함수 같이 간단한 식으로 한 이유는 이해를 돕기 위해서 입니다만, 사실 본함수가 삼각함수이든 혹은 기함수,우함수가 아닐경우에도 역시 풀이법은 동일합니다.
푸리에 적분을 이용하면 일반적으로 쉽게 풀리지 않는 적분을 간단하게 구할수있는 경우가 많습니다. 가령
(sinx)/x를 0부터 무한대까지 정적분을 하라고 하면 부분적분법으로 무한개의 항이 나옵니다. 어디서 급수가 수렴하는지도 알기 어렵습니다.
하지마 푸리에 적분을 이용하면 위함수가 파이/2 즉 90도에 수렴한다는 것을 알수있습니다.
문제를 하나더 풀어봅시다.

위에서 나온 푸리에 계수를 푸리에 적분식에 대입하면 끝입니다.
대입하는 것은 직접해보시길 권합니다. 수학은 자기손으로 풀어야 자기자신의 것이 됩니다.
이후 푸리에 적분을 이해했다면 푸리에 변환도 쉽게 느껴지실것 같습니다.
'mathematics > engineering math' 카테고리의 다른 글
| 수학에서 정의하는 공간과 차원의 개념 (0) | 2019.03.31 |
|---|---|
| 푸리에 변환(Fourier transform) (2) | 2019.03.31 |
| 편미분 방정식의 경계값 문제 -수학적 모델링 (0) | 2019.01.17 |
| 편미분 방정식의 풀이법(PDE) (0) | 2019.01.17 |
| 편미분 방정식(PDE) (0) | 2019.01.17 |


