권찡's 공학이야기
푸리에 변환(Fourier transform) 본문
푸리에 변환 역시 이전에 한 푸리에 급수를 적분으로 변환한 것과 비슷합니다.
어쩌면 라플라스 변환같은 변환식인것이지요. 하나의 예를 들자면 시간축으로 표현된 함수를 주파수축으로 표현하기 위해서 푸리에 변환을 사용하기도 합니다.
푸리에 변환은 급수를 오일러 공식을 통해서 변환합니다.
오일러 공식이 무었이냐?
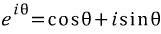
위와 같은 공식을 오일러 공식이라고 합니다. 이식은 매클로니 급수를 통해서 증명이 가능합니다. 기본적인 매클로니 급수를 보여주면
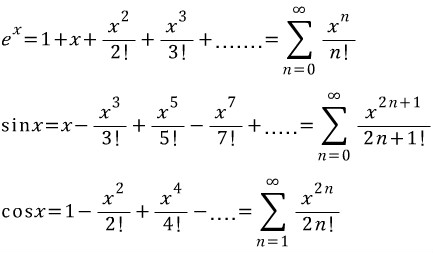
위 메클로니 급수를 오일러 공식에 대입해면 오일러 공식이 성립하게 됩니다.
그렇다면 오일러 공식을 통해서 삼각합수를 표현할수도 있습니다.

이런 오일러 공식을 통해서 이전에 푸리에 급수를 표현할 수 있습니다.
잘 이해가 안되는 분들을 위해서 설명을 하면

자 다시 본론으로 돌아와 푸리에 급수는 아래와 같았습니다.
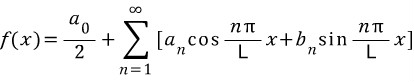
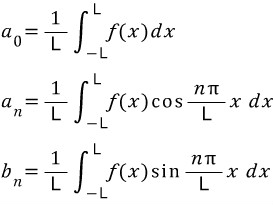
코사인과 사인 함수의 결합으로 표현되있는 것을 오일러 표현으로 바꿔면 됩니다.

오일러 표현으로 고친 푸리에 급수입니다. 이식을 다시 푸리에 적분과 같이 뮤를 이용해서 고치겠습니다.
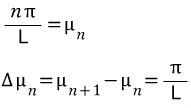
그러면 위 오일러 공식으로 표현된 푸리에 급수는 아래와 같이 다시 쓸수 있습니다.

구간 L을 무한대로 확장하면 푸리에 변환식을 얻게 됩니다.
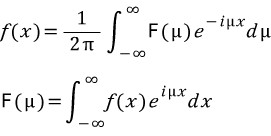
결론으로 도출된 2개의 식이 푸리에 변환식이며 푸리에 역변환식입니다.
첫번째 식이 푸리에 변환된 식이 이미 존재 했을때 원래의 식을 찾는 역변환식, 2번째 식이 원함수를 푸리에 변환시키는 식이 됩니다.
이 2개의 식의 도출과정은 잊어 버려도 상관 없으나 결론식을 외워두셔야 합니다. 푸리에 변환은 많은 분야에서 활용되고 있습니다.
회사에서 일을 한다면 푸리에 변환시켜주는 프로그램이 있긴 있습니다만, 알고 하는 것과 모르고 하는 것은 차이가 크다고 봅니다.
이렇게 푸리에 변환은 라플라스 변환과 같이 기호로 푸리에 변환을 의미하는 것이 잇습니다.

이처럼 약간 이텔릭체로 F를 쓰는 것이 푸리에 변환의 수학적기호입니다.
공학에서 주요하게 사용하는 함수는 삼각함수입니다. 이전에도 사인급수 코사인 급수 등등으로 나눴던것 처럼 푸리에 변환 역시
푸리에 코사인, 사인 변환을 알아봅시다. 이전과 마찬가지로 기함수,우함수의 특성을 이용한것입니다.

마찬가지로 원함수f(x)가 기함수라면 위의 과정을 통해서 구할수 있습니다.
과정은 생략하고 결론을 살펴봅시다.

일반 푸리에 변환에 우함수 기함수의 특징을 넣고 그것을 사인과 코사인의 오일러 공식을 이용해서 구하는 것입니다.
코사인 사인 변환은 푸리에 적분에서 푸리에계수와 사실상 모양이 같습니다.
예제를 하나 풀면서 푸리에 변환을 익히고 다음장으로 넘어가도록 합시다.

정의로 푸는 방식입니다. 그러나 원함수 f(x)는 생각해보면 y축에 서로 대칭인 우함수의 특징을 나타내고 있습니다. 그렇다면 푸리에 코사인 변환을 통해서 푸는 것도 가능하죠

f(x)가 우함수나 기함수가 아니라면 정의에 의해서 풀어야 겠지만 기함수나 우함수일경우는 코사인 변환이나 사인 변환을 이용해서 푸는 것이 더욱 빠릅니다.
이런 푸리에 변환은 미분방정식의 해를 구하는데 이용하기 위해서는 도함수의 푸리에 변환도 알아야겠죠
단 조건이 있습니다.
x-> 무한(infinity) 일때 f(x)=0 ,f'(x)=0 이 되야됩니다.
즉 함수가 수렴해야한다는 조건이 있을때 도함수를 푸리에 변환할수 있습니다.
식을 써서 알아봅시다.

2계 도함수의 경우 역시 동일한 과정을 통해서 구할수 있습니다. 이런 과정을 일반화시키면 아래 식을 구할수 있습니다.
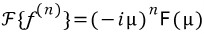
그렇다면 f함수가 기함수 혹은 우함수 일경우, 삼각함수의 푸리에 변환을 이용하는데 이런 f함수가 미분되어있다면
우리는 부분적분법을 통해서 구할수 있게 됩니다.
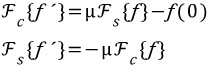
즉 한번 미분된 함수를 푸리에 코사인 변환을 하면 푸리에 사인 변환식이 나오게 되고, 푸리에 사인 을 취하면 푸리에 코사인 식이 나오게 됩니다.
2번 미분된 함수는 어떨까요???
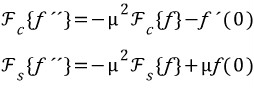
위 식에서 알수 있는 것은 뭔지 생각해봅시다.
위 사인 변환및 코사인 변환은 풀려고 하는 문제의 정의역의 변수중에 적어도 하나는 반무한 구간이어야 이용될수 있다는 것과
일반 푸리에 변환의 경우 정의역이 실수 전체일때 이용할수 있습니다. 때문에 문제에서 구간이 어떻게 주어지는지에 따라서 적절하게 선택해서 풀어야한다는 의미입니다.
위처럼 상미분이 아니라 편미분의 경우는 이전에 2변수함수의 라플라스 에서 다룬것 처럼 하면 됩니다. 즉
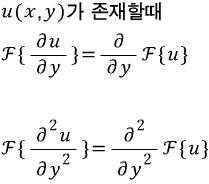
왜 이렇게 되나면 일반적으로 푸리에 변환은 x에 관해서 적분하는 식입니다. 다시 한번 푸리에 변환의 정의식을 떠올리시면 이해할수 있을 것입니다.
도함수의 푸리에 변환도 다뤄봤으니 미분방정식을 한번 푸리에 변환으로 풀업보시다..

이 문제는 기본적인 열전도 방정식 문제입니다. 이전에 분리해로 나눠서 풀거나 혹은 라플라스 변환을 통해서 풀었습니다.
이번에는 이 열전도 방정식을 푸리에 변환을 통해서 풀어봅시다.
이 문제는 무한히 긴 배관이라고 생각할수 있습니다. 양변에 푸리에 변환을 취해봅시다.


이 초기 조건을 일반해에 대입하면

마지막 부분에 허수부가 기함수인것에 대한 설명은 역변환식 붙는 오일러 지수에 허수부 즉 사인함수부분과 초기조건을 대입해 구한 사인함수가 있기때문에 허수부가 0이 되는 것입니다.
'mathematics > engineering math' 카테고리의 다른 글
| 공학에서 Fourier Series,Transform (0) | 2019.03.31 |
|---|---|
| 수학에서 정의하는 공간과 차원의 개념 (0) | 2019.03.31 |
| 푸리에 적분 (1) | 2019.03.31 |
| 편미분 방정식의 경계값 문제 -수학적 모델링 (0) | 2019.01.17 |
| 편미분 방정식의 풀이법(PDE) (0) | 2019.01.17 |



