권찡's 공학이야기
르장드르(Legendre) 방정식과 다항식(polynomial) 본문
앞서 다룬 스튀름-리우빌 이론 (간단한 설명) 의 대표적 예로 르장드르 방정식이 있었습니다.
아래와 같은 꼴의 미분 방정식을 르장드르 미분방정식이라고 합니다.

여기서 n은 상수입니다. 음이 아닌 양의 상수
스튀름-리우빌 형식으로 쓰면

위 식은 x가 1,-1,무한 에서 정칙 특이점을 가집니다. 하지만 이 점들 대신에 x=0 주변에서의 해의 행동에서만 관심을 갖겠습니다.
왜냐하면 x=0 주변에서의 해 들이 물리나 공학에서 더 의미 있기 때문입니다.
x=0 일때 정상해를 가지기 때문에 아래의 식을 위 르장드르 미분방정식에 대입하면


이러한 형태의 식을 얻을수 있습니다. 이 식에서 우변의 0이 되려면 계수 부분이 0이 어야 하기 때문에 식을 정리하면 아래와 같은 순환 공식을 얻게 됩니다.

여기서 c0와 c1이 임의의 상수일때 2배수(C_2k)일때는 c0와 관계가 있고, 홀수(C_2k+1)일때는 c1와 관계가 있습니다.
따라서 다음과 같은 일차 독립인 2개의 급수해가 존재합니다.

위 식에서 n=0 또는 짝수이면 y1(x)는 유한 급수, 즉 다항 함수가 되고, 양의 홀수이면 y2(x)가 다항함수가 됩니다.
x=1 일때 이런 각 다항 함수의 값이 1이 되도록 미정계수 c0,c1의 값을 적절히 정한 것을 르장드르 다항함수라고 합니다. 그리고 이것이 르장드르 미분방정식의 해가 되는 것이죠
예를 들면 아래와 같이 됩니다.

n=1,2,3,4,5 인 경우 구간 [-1,1]사이에서의 르장드르 다항식의 그래프는 아래와 같습니다.
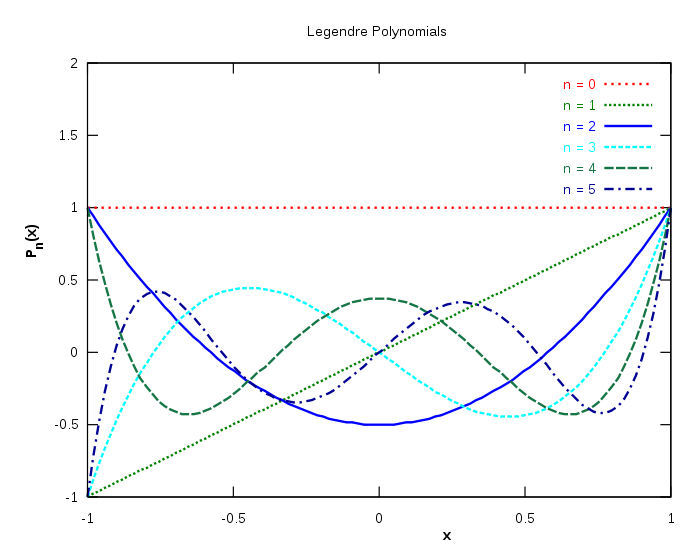
이런 르장드르 다항 함수는 외우고 있다면 편리하겠지만, 쉽진 않습니다. 어렵죠
당연히 일반적으로 공식화 시켜놓은 것이 있습니다. 로드리게스(Rodrigues)의 공식이라고 하여 아래의 식입니다.

위 다항식은 몇가지 성질을 가지고 있는데 쉽게 유추할수 있습니다.


또한 르장드르 다항힉 낄 구간 [-1,1]에서 L^2 내적을 취하면 다음과 같은 결과를 얻게 됩니다.

뒤에 델타는 코로네커 델타라고 해서 선형대수학에서 정수값을 가지는 두개의 변수에 대해서 정의된 함수입니다.
간단히 정의 내리면 아래와 같습니다.

즉 르장드르 다항식은 구간 [-1,1]에서 서로 수직함을 알수 있습니다. 이는 르장드르 방정식이 스튀름-리우빌 문제에 속하기 때문입니다.
르장드르 미분 방정식을 다시 스튀름-리우빌 방식으로 정리한것을 보면

람다가 들어가야할 자리에 n(n+1) 이 있는 것을 알수 있고, 이것이 고유값임을 알수 있는 것이죠
자!~ 지금까지 본 내용은 제 1종 르장드르 함수 입니다. 제 2종도 존재하지만, 스튀름 리우빌 이론을 재정리(심화내용)할때 다루죠.
'mathematics > engineering math' 카테고리의 다른 글
| 라플라스 변환(미분.적분형태)-제2 변이 공식 (0) | 2019.01.08 |
|---|---|
| 라플라스 변환&역변환 (0) | 2019.01.08 |
| 스튀름-리우빌 이론(Sturm-Liouville Theory) ver.1 (2) | 2018.11.08 |
| 미분방정식(ODE) 풀이-프로베니우스 해법 (0) | 2018.11.08 |
| 연립 미분방정식 여러가지 Solution (0) | 2018.10.31 |
