권찡's 공학이야기
Complex number(복소수) - 2편 복소해석함수 본문
이번장은 해석함수에 대해 알아보겠습니다.
먼저 해석적 이라는 말의 의미를 알아야겠죠.
간단히 말하자면 복소함수f가 임의의 복소수 z에 대해서 미분가능하면 해석적이라 합니다. 영어로 analytic 이라합니다.
수학에서 해석함수는 국소적으로 수렴하는 멱급수로 나타낼 수 있는 함수를 말합니다. 이 말은 임의의 한 z 근방에서 테일러 급수가 수렵하는 것과 같은 의미이고, 정의역 D의 모든 점에서 해석적인 함수를 해석적이라 합니다.
복소수라해서 미분가능의 의미가 바뀌는 것은 아닙니다. 만약 모든 복소수에 대해서 미분가능하다면 전해석 또는 완전해석이라 합니다.
이를 판별하기 위해서는 아래의 코시 리만 방정식을 사용합니다.
#코시 리만 방정식

즉, 위 방정식이 성립하면 복소함수f는 해석적이라 할수 있습니다. 좀 더 나아가면 복소함수f가 해석적이 될때(코시 리만 방정식이 만족할 때) 실수부u와 허수부v는 서로에 대한 공액조화함수라 합니다.
이 공액조화함수는 라플라스 방정식을 만족하며, 라플라스 방정식을 조화함수라 부르게 됩니다.

예를 들면 아래의 경우입니다.

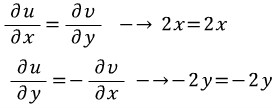
조화함수 식에 대입하면 0이 나와 라플라스 방정식이 성립함을 알 수 있죠.
선적분과 면적분을 할 줄 아신하면 함수가 보존적이라 하면, 경로와 상관없이 선적분을 해도 값이 동일하다는 것을 알고 있을 것입니다. (면적분, 선적분 내용은 다음장에서 나올 내용이니 일단 몰라도 됩니다.)
위에서 해석적인 함수를 가지고 연습해 봤다면 이번에는 해석적이 아닌 함수의 경우를 봅시다.

위 복소함수는 코시리만 방정식이 성립하지 않죠. 따라서 해석적이라 할 수 없습니다.
연습한번 해보죠.
코시리만 방정식과 조화함수를 이용해서 공액조화함수를 찾아봅시다.

위 함수가 해석적이라는 조건을 이용해서 구해봅시다.

임의로 제가 만든 문제라서 상수값은 정확히 나오질 않네요.
그렇다면 정확히 정하는 것이 가능한 문제로 해봅시다.

풀이 과정을 써보면



# 초등 해석함수
이번에는 지수함수 및 로그함수 등 초월함수에 대해서 알아보죠.
먼저 지수함수를 봅시다.

어떤 복소수를 지수형태로 표현한 것이 아닌 지수부분에 복소수가 들어가 있는 경우입니다.
공학을 전공했다면 아래의 표현도 많이 보셨을 것입니다.

이런 지수가 복소수인 함수는 전해석함수입니다. 즉 어떠한 복소수에 대해서도 해석적이라는 말입니다.
복소수가 들어가있다해도 쫄 필요는 없겠죠. 그러나 주편각을 고려해야하긴 합니다.

지수에 복소수가 들어있는 맨 처음 식은 삼각함수의 크기가 1이기 때문에 절대값 즉 크기가 exp[x]가 됩니다. 삼각함수 부분이 편각을 나타내는 것이기 때문에 자명하게 y가 편각이 되는 것입니다.
예를 들어야 이해하기 편하겠죠.

위와 같이 풀어도 무관합니다. 사실 직관적으로 풀릴 만큼 쉬운 값이기 때문에 보자마자 편각이 60도 인것을 눈치채는 것도 가능합니다. 난이도 좀 높여보죠. 앞서 배운 사상과 섞어보겠습니다.

해결하기 어려워 보일 수도 있습니다만, 기초가 되는 개념을 이해했다면 푸는 것이 가능합니다.

3번의 경우도 개념을 이용하면 됩니다.

그렇다면 로그함수의 경우는 어떤지 봅시다. 위의 지수함수 개념을 응용하면 됩니다.

중간 과정을 생략하고 중요하게 알아볼것만 알아봅시다.

개념이 조금 왔다갔다가 해서 어려울수 있으니 추가 설명을 하면

위에서 설명한것 처럼 logz는 주값이라고 하면 다가함수입니다 여기서 z가 0이 아닌 복소수에 logz의 주값을 대응시키는 함수가 주 로그함수입니다.
주 로그함수는 대문자 L을 써서 Log z로 나태나게 되고 결과적으로 아래와 같은 식으로 표현할수 있습니다.

예를 통해서 이해를 해봅시다.

다른 예를 들면

조금만 더 응용해봅시다.
복소수에 거듭제곱 꼴에 대해서 알아봅시다.
위에 했던 내용과 많이 겹치는 내용으로 어려울게 없습니다.

이렇게 표현하는 방법의 관계식으로 정의됩니다. 이전에 제가 복소함수 문제 풀이 할때 마지막에 언급한 방법과 동일한것이죠
복소수의 로그함수를 배웠으니 적용을 해보자는 것입니다.

이 방법이 사실상 이전의 문제풀이에서 햇던 방법과 동일한 것이죠

이런 방식으로 했다면 이제는 로그함수를 알고 있으니 좀더 편하게 할수 잇는 것입니다.

위의 방법으로 풀든 아래의 방법으로 풀든 답은 같습니다. 복소로그함수에 익숙해지면 아래방법이 더 편할것입니다.
마지막으로 삼각함수나 쌍곡선함수를 정리하고 이번장을 마치죠
이전에 최초로 오일러 공식을 설명할때 코사인함수와 사인함수를 오일러 공식으로 표시한적이 있습니다.

복소수가 들어갔다고 해도 삼각함수의 미분및 적분 공식은 그대로 적용됩니다. 합차 공식도 마찬가지로 적용되죠
쌍곡선 함수 역시 마찬가지로 복소수가 들어간것 뿐 공식으로 사용되는 식들은 변홤이 없습니다.
추가로 외워야 될 부분만 하고 넘어가면

쌍곡선함수와 삼각함수간에 위와 같은 공식이 성립하게 됩니다. 일반적으로 실수를 다룰때는 위 공식은 성립하지 않으나
복소수로 넘어오면서 삼각함수를 오일러 공식을 통해 지수함수로 표현이 가능해지면서 쌍곡선함수와 연관성이 생긴것이라고 보면 됩니다.
쫌 쉬운 한가지 예를 들어서 복소수 삼각함수를 봅시다.

이 문제를 굉장히 간단한 문제입니다. 위에서 언급한 공식을 적용하면 바로 풀수 잇죠

초등해석함수는 이걸로 마치고 다음에 들어갈 유수정리나 레시드 이런것을 하기위해 알아야할 선적분, 면적분에 대해서 언급하고 지나가겠습니다.
'mathematics > engineering math' 카테고리의 다른 글
| Complex number(복소수) - 3편 복소함수 선적분 (0) | 2019.10.29 |
|---|---|
| 선적분과 면적분(Line integral, Surface integral) (1) | 2019.10.29 |
| Complex number(복소수) - 1편 복소함수 (0) | 2019.10.28 |
| Complex number(복소수) - basic편 (0) | 2019.09.09 |
| 퓨리에 변환의 성질과 라플라스, Z-변환 관계 (0) | 2019.09.09 |




