권찡's 공학이야기
Complex number(복소수) - 1편 복소함수 본문
복소수 역시 실수와 마찬가지로 함수가 존재합니다. 이번장은 이런 복소함수(complex function)에 대해서 알아봅시다.
가장 알기 쉬운 원부터 해보죠.
복소평면 상의 원은 아래와 같은 방식으로 표현합니다.

이때 z0는 임의의 복소수입니다. 절대값이 취해져 있으니 r은 크기가 되겠고, 이는 거리(반지름)을 나타내죠. 가장 쉬운 예를 하나 들어보죠


처음 원에 대해서 배울 때 혹은 원 좌표계에 대해서 배울 때 위와 같은 표현 방식을 알게되죠. 그렇다면 위 수식을 부등식으로 바꾼다면 어떻게 될까요?

이 말은 위 복소평면상에 나타난 원의 내부를 말하게 됩니다. 부등식이 1을 포함하지 않기 때문에 위 원의 테두리는 포함되지 않습니다. 이를 개원판(Open Disk)라 합니다. 반대로 1을 포함하고 있다면 닫힌원판이라 하며 유한집합이 됨을 알수 있죠.
만약 z0=1+i 였다면 그만큼 원을 평행이동하면 되는 개념입니다.
이런 복소평면 상의 함수를 복소함수라 하며 보통 아래와 같이 씁니다.

즉, 어떠한 함수에 복소수가 들어있는 경우를 말합니다. 이때 복소수 z가 복소수 w로 사상, 변환 했다고 표현합니다.
위와 같은 사상에 대해서 몇가지 알아봅시다.
#선형 사상

위 경우 복소수가 어떻게 변화될까요? 위 경우는 복소수가 평행이동과 회전을 같이한 경우입니다.

즉, w를 복소평면상에 표현하면 아래와 같이 되죠

벡터의 합과 비슷한 형태가 됩니다. 그렇다면 a가 1이 아닌 복소수의 경우라면 회전의 개념이 됩니다.
이 회전을 이해하기 위해서는 복소수를 표현하는데 있어서 복소지수형을 알아야 합니다.

오일러 공식과 비슷한 면이 있기 때문에 오일러 공식을 안다면 쉽게 이해가능하죠. 복소지수형은 모든 복소수를 오일러 공식을 통해 변환가능합니다. 따라서 a가 복소수라 할지라도 지수함수 형태로 나타내는 것이 가능하죠.
이전 part의 극좌표형에서 좀더 나아간 표현이 됩니다. a가 복소수라 할지라도 아래와 같이 사상하면 됩니다.

복소지수형으로 변환하면서 복소수끼리 곱이 간단해집니다. 역시 간단한 예로 이해하면 좋겠죠.


먼저 z 앞의 계수부터 처리해봅시다. 이는 회전을 의미하며 위에서 예를 보인것과 같이 z앞에 곱해지는 계수의 크기만큼 곱한 것이 크기 계수의 편각만큼 회전입니다. 기존 z의 크기는 루트5이며, 곱해지는 계수의 크기는 루트2입니다.

즉, 크기는 루트10이 되는 거죠. 회전에서 부호는 시계방향과 반시계 방향을 나타내며 반시계 방향이 + 입니다. 즉 시계 방향 회전은 아래와 같은 것이죠

여기에 b의 값을 더하는 만큼 평행이동이 됩니다.
이런 회전과 평행이동을 선형사상이라 합니다.
#이차함수의 사상(고차함수)
복소함수가 2차 함수의 경우에도 복소지수함수 형태로 계산하면 간단합니다. 예로 2차사상을 계산합니다.


위와 같이 z가 x+yi 여도 복소지수함수 형태로 계산합니다. 위 결론을 통해 무엇을 알 수 있을까요? 제곱을 하면 편각이 2배가 되며, 복소수의 크기는 2제곱이 됩니다. 만약 3제곱이라면 편각이 3배, 크기가 세제곱이 될 것입니다.
원을 예로 들어본다면 편각이 배가 되는 것을 이해할 수 있을 것입니다.

위 함수를 제곱하면

위와 같이 편각이 2배가 됩니다. 이와 같이 복소수에 대해서 고차로 올릴때 승수가 마이너스 일 경우는 반전이라고 부릅니다. 이런 반전사상은 위와 같이 크기가 배수가 되는 것이 아닌 나눠지는 형태이며 편각도 반대로 됩니다.

이런 반전사상의 한가지 예를 알아봅시다.

위와 같이 정리가 가능합니다. 이때 u,v 정의를 통해 x,y 값을 재정리할 수 있습니다.

이와 같은 방식을 통해 정리된 것을 이용해 아래의 함수 관계가 성립 여부에 따라 사상 후 어떻게 될지 알수 있습니다.

이를 통해 반전은 원 혹은 직선으로 사상된다는 것을 알수 있습니다.
몇가지 예를 들어서 이해해봅시다.

위 문제를 한번 풀어보죠

동일한 방법으로 2번을 풀수 있습니다.

3번의 경우는 위방법대로 하되 부등호만 유지하면 됩니다.

앞서 복소수의 다가성(답이 여러개 존재하는 특성)을 봤었습니다.
이전에 설명한것 처럼 주편각의 개념에 의해서 복소수가 가지는 다가성을 보여준적이 있습니다.
이전에 풀은 방법은 복소수를 오일러 형식으로 고쳐서 주편각을 고려하는 것입니다.
여기서는 다른 방법을 소개하도록 하겠습니다. 문제를 예로 들겠습니다.

위 문제를 푸는 법을 쉽게 설명하겠습니다.


사실상 결과가 같은것이 보이십니까??
즉 지수함수를 이용해서 구하는 방법입니다. 지수 부분에 ln을 붙여서 사실상 같은 수치임에도 저렿게 표현해서 오일러 공식을 적용하는 것이죠
2번과 3번도 풀어봅시다.

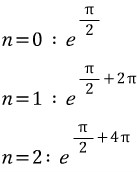
3번 문제는 이전의 복소수의 다가성을 할때 언급한것과 비슷합니다. 복소수 8의 세제곱근은 2만 있는것이 아닙니다.

이런 방법을 이용해서 구할수 있습니다.
조금 응용한 문제를 마지막으로 이장을 마치겠습니다.

풀이


'mathematics > engineering math' 카테고리의 다른 글
| 선적분과 면적분(Line integral, Surface integral) (1) | 2019.10.29 |
|---|---|
| Complex number(복소수) - 2편 복소해석함수 (2) | 2019.10.29 |
| Complex number(복소수) - basic편 (0) | 2019.09.09 |
| 퓨리에 변환의 성질과 라플라스, Z-변환 관계 (0) | 2019.09.09 |
| 공학에서 Fourier Series,Transform (0) | 2019.03.31 |




