권찡's 공학이야기
퓨리에 변환의 성질과 라플라스, Z-변환 관계 본문
이전장에서 연속시간함수의 푸리에 변환, 이산시간함수의 푸리에 변환에 대해서 알아봤습니다.
실제 이런 푸리에 변환을 손으로 계산하는 것은 학생때 직접하겠지만, 실제 엄청난 양의 데이터를 손으로 직접 계산한다는 것은 굉장히 힘들고, 무리입니다.
또한 컴퓨터에서 이런 계산을 대신하기 위해서는 신호가 이산적이어야 합니다.
즉 DTFT가 사용될것 같지만 아래 그림에서 보는 것과 같이 비주기적인 이산함수를 푸리에 변환하면, 연속 주기 스펙트럼이 나타납니다

컴퓨터에서 연속적 신호는 정보량이 굉장히 많기 때문에 오래걸리기도 하고 효율이 좋지 못하겠죠
때문에 샘플링을 추가해서 DFT(Discrete Fourier transform) 을 해야 됩니다.
즉 , DFT란 시간영역의 이산 함수를 주파수 영역의 이산 함수로 변환하는 것을 말하고, 디지털 장치에서 쓰기 위한 푸리에 변환의 한 종류입니다.
FFT는 특정 알고리즘을 도입해서 계산속도를 빠르게 하는 것입니다.
DFT를 하기 전에 먼저 이전에 배운 푸리에 변환에대한 성질을 정리해볼 필요가 있습니다.
기본적인 푸리에 변환의 성질
시간과 주파수의 관계가 1대1로 대응되는 것은 당연하므로 언급하지 않겠습니다.
문제는 시간영역의 함수가 존재하면 반드시 푸리에 변환을 할수있는가입니다.
이전장에 디리클레 조건에 대해서 언급을 했는데, 간단히 말하면 에너지가 무한하면 푸리에 변환을 할수없습니다.
즉

위 조건이 만족해야만 푸리에 변환을 할수 있습니다
즉 시간 영역의 함수가 x^2 같이 무한히 증가하는 경우에는 푸리에 변환이 존재하지 않습니다.
또한 기본적인 푸리에 변환의 식을 생각해보면
지수함수를 곱해서 적분한 꼴의 형태입니다.

여기서 시간 영역함수에 복소지수함수인 e^jWt 를 곱해서 퓨리에 변환을 하게 되면
위상이 변화하는 특징을 갖습니다.
라플라스 변환이나 다른 변환과 마찬가지로 푸리에 변환은 약 12가지 특성이 존재합니다.
1. linearity (선형성)

2. time scaling

3. Duality

4. Time shifting

5. Frequency shifting

이 내용은 변조와 복조에 직접적인 상관이 있습니다.
6. Area under g(t)

7. Area under G(f)

8. 시간 축에서의 미분

9. 시간축에서 적분

10. 켤레함수

11~12. 컨볼루션과 관계
여러번 설명한 내용이긴 한데, 시간영역에서 컨볼루션인 것에 푸리에 변환을 하게 되면, 주파수 영역에서는 곱으로 표현되고, 시간 영역에서 곱은 주파수 영역에서 컨볼루션으로 표현되는 것을 말합니다.
마찬가지로 DTFT에서도 거의 동일한 성질을 가지게 되나 다른점은 있습니다.
1. 대칭
푸리에 변환을 하게 될시 대칭성질을 가진다는 것입니다.
즉

위와 같이 정리할수 있습니다.
이때 시간 영역의 함수가 우함수이면 푸리에 변환이 실수함수만 존재한다는 결론이 나오게 됩니다.
2. 시간 반전

3. 시간 이동

4. 주파수 이동성

5. 컨볼루션 성질

6. 곱하기 성질

5번 6번 성질은 사실상 같은 성질이라 봐도 무방합니다.
이외에도 확률에서의 자기, 상호 상관 함수와의 유사성 , 변조, 라플라스, Z-변환과의 관계에 대한 것도 있지만 나중에 따로 다루겠습니다.
설명할 내용이 좀 많습니다.
상관함수와 유사성은 확률에서 다룰 것이고, 변조는 통신에서 다룰 내용이며, 라플라스와 Z-변환은 푸리에 변환을 다 정리하고 나서 다루겟습니다.
차이점은 뭘까요? 그건 바로 상대성 Duality가 DTFT에서 성립하지 않는다는 것입니다.
CTFT에서는

즉
이 되는데
DTFT에서는 성립하지 않습니다.
문제는 바로 이산 시간함수에 대한 푸리에 변환은 무조건 주파수 스펙트럼이 주기함수가 된다는데 있습니다.
간단히 말해서 , 대문자 G는 주파수 영역의 함수입니다. g는 시간영역에서의 함수이고, 이 함수들 간에는 푸리에 변환 관계를 가지지만,
2ㅠ 의 계수값 같은 것이 들어가있습니다.
이산 함수에서 이런 듀얼리티가 성립한다면
시간영역에서 비주기함수 x(n)을 푸리에 변환해서 X(w)를 얻었는데 , 이 함수는 무조건 주기함수가 됩니다. 변수를 다시 시간 n으로 바꾼다고 해서 X(n)이 비주기함수를 포함할수 없다는 것입니다.
성질의 차이는 상대성 말고는 없네요.
이번에는 다른 변환과의 관계에 대해 알아봅시다.
위에서 말한 푸리에 변환은 라플라스 변환,Z-변환과 어떤 관계가 있을까요???
먼저 라플라스 변환의 식은 아래와 같죠

CTFT의 식은 아래와 같습니다.

식이 유사성을 가지는 것을 알수있습니다.
즉 라플라스 변환의 s 는 j2ㅠF 와 동일하다는 것을 알수있습니다.
라플라스 변환을 하면 , 우리는 s평명이라고 해서 복소평면을 이야기 합니다.
즉 s는 복소수를 나타내는 것입니다.이 복소수의 허수부가 앞서말한 주파수와 같습니다.
s= j2ㅠF라고 했으니 이것을 s평면에 그리게 되면 F가 실수이므로 s평면에 허수축을 나타냅니다.

즉 허수축에서 구한 라플라스 변환이 퓨리에 변환이라는 소리입니다.
범주로 따지게 되면 라플라스 변환이 연속시간 푸리에 변환보다 큰 집합이라는 말이 됩니다.
물론 더 깊게 들어가서 수렴 영역도 정의 할수 있습니다.
가령 U(t): unit step 함수를 변환해봅시다.
그러면 푸리에 변환은 존재할것인가
결론부터 말하면 존재하지 않죠. 당연히 수렴하지 않는 함수이기 때문에 존재하지 않습니다. 앞서 말햇듯이 적분을 취했을시 무한하지 않아야 하는것이 푸리에 변환의 조건입니다. 즉 유한한 에너지 값을 가져야 한다는 것이죠
식으로 풀어서 써보면

그렇다면 라플라스 변환이라면

이말은 곧 푸리에 변환의 실지수함수가 곱해진 꼴이 라플라스 변환임을 나타내며
S 평면에서 실수가 양수일때만 성립한다는 것을 알수있습니다.
푸리에 변환은 이런 실수가 0인 것을 나타내며 이는 허수축이라는 것을 말하는 것이죠.
이번에는 Z-변환과 DTFT의 관계를 알아봅시다.
Z-변환은 이산 함수의 차분방정식을 풀때 사용되는 수학적툴입니다. s평면과 마찬가지로 z평면이 존재하는 것이죠.
이산 함수에 대한 z변환은 아래와 같이 쓸수 있습니다.

DTFT의 식은 아래와 같았죠

라플라스 변환과 마찬가지로 유사성이 보입니다.
즉

복소지수함수의 크기가 1이며, 위상이 변함에 따라서 단위원이 그려집니다.
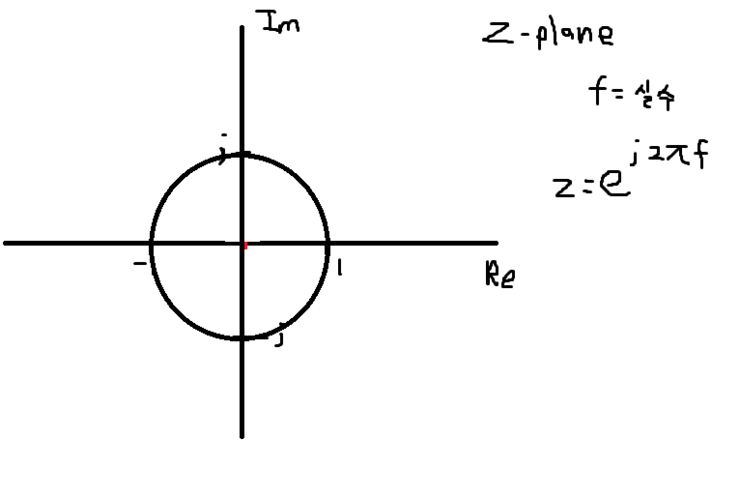
DTFT은 단위원에서 z변환을 구한것이 됩니다.
라플라스 변환과 마찬가지로 z변환이 좀더 큰범주가 되는 것입니다.
이때 이산 정현파, 이산적인 삼각함수는
3가지 특징을 가지는데
1. 주파수가 유리수인점에서 주기가 된다.
2. 주파수f가 1/2에서 최대 주파수를 갖는다.
3. 주파수f 는 1 마다 주기성을 갖는다.
입니다.
위의 z평면에서 그것을 확인해 보면
f = 1/2 인 점은 실수가 -1 , 허수가 0인 점을 말합니다. 즉 이때 가 가장 높은 주파수를 갖는다는 것이죠
주기성은 당연히 위상이 다시 되돌아오므로 당연한 것이죠
위에서 처럼 계단 함수를 예로 들겠습니다.
이산적인 계단 함수를 가지고 DTFT과 Z변환을 해봅시다.

역시 마찬가지로 수렴하기 위해서 조건이 필요하죠
ROC : 공비의 절대값이 1보다 작아야 함

즉 z평면 상에서 단위원의 외부 영역이 수렴 영역 입니다.
즉 이산 퓨리에 변환은 단위원에서의 z변환을 나타낸다고 말할수 잇겠네요.
나중에 공학 정리할때 시스템에 대해서 정리하게 되면 입력과 출력의 관계에 따른 전달함수의 pole과 zero도 매우 중요한 요소이지만 공학수학에서 다룰 필요는 없을것 같습니다.
굳이 시스템의 전달함수를 정리할 필요가 있나 싶기도 하고, 다들 잘 아는 내용이니 별로 필요 없다고 생각되기도 하네요.
정리를 해보면
CTFT에서 라플라스의 수렴 영역에 허수축이 포함된다면 수렴하게되고,
DTFT에서 z-변환의 수렴 영역에 단위원이 포함된다면 수렴하게 된다는 것입니다.
수렴한다는 말은 곧 , 퓨리에 변환이 존재할수 있다는 말과 같은 말이니깐요.
'mathematics > engineering math' 카테고리의 다른 글
| Complex number(복소수) - 1편 복소함수 (0) | 2019.10.28 |
|---|---|
| Complex number(복소수) - basic편 (0) | 2019.09.09 |
| 공학에서 Fourier Series,Transform (0) | 2019.03.31 |
| 수학에서 정의하는 공간과 차원의 개념 (0) | 2019.03.31 |
| 푸리에 변환(Fourier transform) (2) | 2019.03.31 |




