권찡's 공학이야기
2계 미분방정식-Nonhomogeneous Differential Equation(미정계수법) 본문
2계 미분방정식-Nonhomogeneous Differential Equation(미정계수법)
권찡 2018. 10. 30. 20:13이번에는 비제차 미분방정식의 풀이를 정리해보겠습니다.
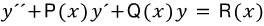
위와 같은 표준형에서 우변의 R(x)항이 0이 아닐경우 비제차(Nonhomogeneous)라고 합니다.
이러한 비제차 미분방정식의 해를 구하는 법을 정리하기 앞서 해에 대해서 정리하고 갈 내용이 있습니다.
제차 미분 방정식 , 즉 R(x)=0 일때 해를 구한 것을 우리가 homogeneous solution (제차일 경우 구해지는 해) 라고 하죠.
그리고 우변 R(x)에 대해서 구해지는 해, 즉 비제차의 경우 구해지는 해를 particular solution, 특수해라고 합니다.
이때 양쪽 해의 상관 관계에 대해 설명을 먼저 해야될것 같습니다.
#중첩의 원리
합수 y1, y2, y3 ......... yk가 n계 제차 선형 미분 방정식의 해라면 임의의 상수 cn(n=1,2,3,4,5,6,.......)에 대해서
y= c1y1 + c2yc2+ c3y3 + .............. 이런 형태의 일차 결합 형태 역시 미분 방정식의 해이다
위와 같은 중첩의 원리는 비제차의 경우 homogeneous solution와 particular solution 의 일차 결합도 역시 해임을 말합니다.
(독립과 종속을 따져봐야 될 내용이지만 )
다시 말하면 R(x)가 0 일때와 아닐때 양쪽 모두 해당 미분방정식의 해가 된다는 말입니다. 따라서 비제차 미분방정식의 경우에는 일단 제차 미방의 해 homogeneous solution을 구한수, R(x)에 의한 particular solution을 구한후 일차결합을 통해서 해를 구할수 있는 것입니다.
바로 예를 들어서 알아봅시다.

위 미분 방정식의 homogeneous solution 은 아래와 같이 구해집니다.

여기에 particular solution을 더하는 것으로 해를 구할수 있다는 것입니다.
이런 particular solution을 구하는 방법은 여러가지가 있습니다. 일단 하나하나씩 설명하는 것이 좋을 것 같습니다.
**미정계수법**
일단 가장 대표적으로 미정계수법이 있습니다.
미정계수법이란 particular solution 이 R(x) 형태와 비슷한 형태를 취할것이라는 가정에서 미지수를 놓고 특수해를 구하는 것입니다.
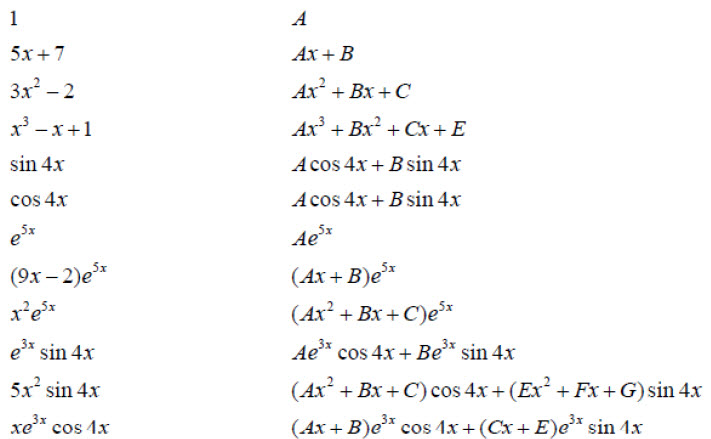
R(x)의 형태에 따라서 상수항이라면 미지의 상수로
일차 함수라면 미지의 계수를 가진 일차 함수로
삼각함수, 지수함수 역시 마찬가지 이며, 결합된 함수 역시 마찬가지 입니다.
이런 식으로 particular solution을 가정해서 미분방정식에 대입해서 계수값을 특정하는 것이 바로 미정계수법입니다.
단, 주의 하셔야 될 내용이 있습니다. 미분방정식에서 p(x),q(x)가 상수항 일때 미정계수법을 해야 편하다는 것입니다.
만일, p(x),q(x)가 상수항가 상수항이 아닌 다른 함수의 형태를 가진경우, 예를 들어서 코시오일러 미분방정식 같은 경우는
미정계수법으로 풀기가 쉽지 않을 것입니다.
때문에 만능으로 손쉽게 풀수 있는 방법은 아닙니다.
'mathematics > engineering math' 카테고리의 다른 글
| 2계 미분방정식-Nonhomogeneous Differential Equation(미분연산자) (1) | 2018.10.30 |
|---|---|
| 2계 미분방정식-Nonhomogeneous Differential Equation(론스키안) (0) | 2018.10.30 |
| 2계 미분방정식-homogeneous Differential Equation (0) | 2018.10.30 |
| 1계 미분 방정식(일반적인 해법으로 풀수 없는 형태) (0) | 2018.10.30 |
| 1계 선형 미분방정식(Linear Differential Equation) (0) | 2018.10.28 |
