linear algebra - 행렬 기초

linear algebra 에서 첫번째로 다룰 내용은 행렬인데, 기본적인 행렬의 특징은 중학교인가, 고등학교인가 처음 행렬을 배울때 했던 내용이니 그것을 다시 하진 않겠습니다.  기본상식으로 깔고 갑니다.

 

먼저 제가 알려 드릴 내용은

 

transpose 와 trace의 개념입니다.

 

 

transpose는 행과 열을 바꾸는 것입니다.

 

기호는 행렬에 윗첨자로 T로 쓰는데,  예시를 보면 이해가 가실 것입니다.

 

 

 

 

 

즉 1행 1열  , 2행 2열,  좀더 큰 행렬이라면 3행 3열 ,  4행 4열 의 원소를 기준으로 바꾸는 연산을 말합니다.

 

 

정사각형 행렬이 아닌 경우는

 

 

와 같이 되는 것입니다.

 

 

또 한가지 방금 말한 1행 1열, 2행 2열의 원소 들을 보고 대각 원소라고 하면

 

 

trace는 이런 대각 원소들의 합을 말합니다.

 

기호는 행렬 앞에 tr을 붙입니다.

 

 

 

이런 특성은 교환법칙이 성립안되는 행렬이랑 헷갈릴수 있는데

 

 

기존의 행렬은 AB=BA가 성립하지 않습니다.

 

그러나

 

 

 

는 성립합니다.

 

비슷한 특성으로 transpose는

 

 

 

가 됩니다.  헷갈리지 맙시다.

 

 

 

아예 trace의 성질을 정리해보면

 

 

가 되는 성질을 가지고 있습니다.

 

 

 

 

자 이제 몇가지 특수행렬을 정리할수 있습니다.

 

 

바로 대칭행렬, 교대행렬,직교행렬입니다.

 

 

1. 대칭행렬

 

대각 원소를 중심으로 위 아래가 같은 행렬을 말하고, 복소 행렬일 경우는 Hermit(허밋 , 에르미트) 행렬이라고 합니다.

 

이 말은 아래의 식이 성립하는 것을 말합니다.

 

 

 

대칭행렬을 만드는 방법은 간단합니다.

 

임의의 행렬 X를 아래의 식을 통해서 대칭행렬을 만들수 있죠.

 

 

 

 

2. 교대 행렬

 

대각 원소를 기준으로 위 아래가 서로 부호가 반대인 행렬을 말합니다. 또한 대각원소가 모두 0 인 행렬을 말합니다.

 

 

대각 행렬을 만드는 방법은 역시 임의의 행렬이 존재할때

 

 

 

 

 

 

위에서 말한 2가지의 특수행렬을 가지고 임의의 행렬을 분해가 가능합니다.

 

 

즉 임의의 행렬 Y를 교대 + 대칭 행렬로 분해가 가능하죠

 

 

 

 

 

3. 직교행렬

 

행렬의 transpose한 행렬이 역행렬이 되는 행렬을 말합니다.  즉

 

 

복소 행렬일 경우 유니터리 행렬이라고 부르며 ,

 

 

이런 직교행렬은 행렬값의 크기가 1이며,

 

각 행, 열의 크기가 1 , 내적은 0 이됩니다.

이때 행 열을 나열시킨 집합은 정규 직교집합의 기저라고 합니다.

 

 

말이 조금 어려우니 예를 들면

아래의 행렬이 직교 행렬입니다.

 

 

특히 2x2 행렬에서는 직교행렬이 위의 경우 밖에 존재하지 않습니다.

 

 

위 행렬은 다르게 부르는 말이 있습니다. 바로 회전 행렬인데  좌표 평면상의 어떤 점을 어떤 각을 가지고 회전시킬 것인지를 나타내는 행렬이기도 합니다.

 

 

이제 위 3가지 특수행렬에 대해서

헷갈리는 성질을 정리해보면

 

 

 

 

위 3가지 특수 행렬은 반드시 기억해 놓으셔야 합니다. 앞으로 많이 나올꺼니

 

 

 

 

 

 

 

자 이번에는 행렬식을 정리해봅시다.

 

??  행렬식 누구나 다아는거 생략한다고 했는데 왜 하는건지?? ,

 

 

행렬식의 5가지 성질 보고 나서 결정하세요. 이중에 모르는것이 있다면 제대로 모르고 있는 것입니다.

 

 

기본적으로 행렬식은 아래와 같이 씁니다.

 

 

 

 

이런 행렬식은 여러가지 성질이 있지만 반드시 기억해야될 성질이 있죠

 

 

 

위 성질 전부 알고 있다면 설명 안들으셔도 됩니다.

 

#첫번째 성질이야 transpose한다고 해서 행렬식이 바뀌지 않는다는 단순한 의미입니다.

 

 

#두번째 성질은 예를 들어서 설명하면

 

 

 

 

#세번째 성질은 행렬식을 구할때 공통인수를 밖으로 꺼낼수 있다는 의미입니다.

 

 

 

 

#네번째 성질과 5번째 성질은 조금 연관성이 있는데.

 

먼저 5번째 성질을 해봅시다.

 

 

 

이런 성질이 5번째 성질입니다.

 

 

이때 4번째 성질은 비례관계 즉 하나의 행에 배수를 해서 더하거나 빼면 그 행의 원소값이 0 이 되는 것을 말합니다.

 

 

 

 

 

 

이런 성질 전부 알고 있었다면 행렬식에 대해서 전부 알고 있다고 말하셔도 됩니다. 할말이 없어요.ㅋㅋ

 

 

 

이런 행렬식의 손으로 하는 계산은 2by2일때는 매우 쉽지만 행렬의 크기가 커질수록 힘들어 집니다. 구하는 몇가지 방법을 알려드리겠습니다.

 

 

1. 라플라스 전개

임의로 하나의 열이나 행을 택해서 각 원소와 그 원소의 여인수를 곱하여 모두 합하는 방법입니다.

 

3by3을 예로 들어보겠습니다.

 

 

 

 

 

 

 

근데 이방법으로 하면 4by4에서 부터는 정말 암걸릴정도로 여행렬이 다시 3by3이 되므로 거의 암걸릴 것 같은 계산을 반복해야됩니다.

 

따라서 위에서 언급한 5번째의 성질을 이용해서 계산을 편하게 만들수 있습니다.

 

이러면 이제 라플라스 전개가 매우 간단해 집니다. 1행의 원소의 여행렬이 매우 간단해지고, 심지어 1행의 원소인 2,3 의 여행렬 행렬식 값은 0 입니다.  따라서

 

 

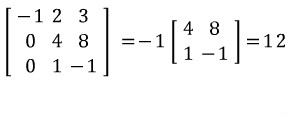
이렇게 구할수 있습니다.  나중에 고유치 나오면 더 쉽게 풀수 있습니다만 고유치 다룰때 합시다.

 

 

 

#역행렬

 

역행렬에 대해서도 정리해봅시다.

역행렬이란 기존의 행렬에 곱해서 단위 행렬이 나오게 하는 행렬을 역행렬이라고 합니다.

 

정의를 해보면

 

 

 

 

여기서 수반행렬은 뭘 의미할까요

 

2 by 2 행렬이라면 다들 알고 있듯이

 

자리바꾸고 , 부호 바꾸고  하는 식으로 할수있습니다.

 

3by 3이라면???

 

쉽지 않습니다.

 

 

이에 수반 행렬에 대해서 알아봅시다.

 

 

예를 들어서 하는것이 좋을 것 같네요

 

3 by3 행렬로

 

 

요런식으로 구하는 것입니다.

 

그렇게 구하게된 행렬을 전치시키면 됩니다.

 

 이 됩니다. 이 것을 행렬식 값으로 나누게 되면

 

 

역행렬을 얻게 됩니다.

 

물론 행렬식의 값이 0이 아니여야만 정칙 행렬이 되겠죠. 

 

 

 뭐 역행렬과 행렬식을 미리 알고 있다면 2가지를 곱하는 것으로 수반행렬을 구할수도 잇습니다.

 

그럼 역행렬의 성질을 알아볼까요

 

 

 

이런 성질을 이용한 하나의 재미있는 식이 바로

 

 입니다.

 

수반행렬의 수반행렬 이라는 것인데 물론 이것을 직접 할 필요 없이 구하는 것이 가능합니다.

 

 

ㅋㅋㅋㅋㅋㅋㅋ

 

퍽이나 재밌겠네 .  여기까지는 수반행렬을 이용한 역행렬을 구하는 원칙대로의 역행렬을 구하는 방법입니다.

 

​

​

​

​

 

좀더 쉬운 가우스 소거법으로 역행렬을 구할수 있는 것을 알려드리겠습니다,

 

 

우리가 구하려는 행렬에  바로 옆에 단위 행렬이 있다고 행각해봅시다.

 

 

 

우리가 행렬식을 구할때 어떤 행이나 열에 정수배를 해서 다른 행과 합과 차를 해도 행렬식의 값이 변하지 않는다는 알았는데, 

 

왼쪽에 있는 행렬을 위의 성질같이 해서 단위행렬로 만들고 , 그 수행된 연산을 동일하게 오른쪽의 단위 행렬에도 수행해 봅시다.

 

 

 

이런식으로 왼쪽의 행렬이 단위 행렬이 될때 까지 연산을 하면 됩니다.

 

 

 

마지막으로 1행을 1이 되도록 2/7 을 곱하게 되면  왼쪽의 행렬은 단위 행렬이 되고, 오른족의 행렬은 아래의 행렬이 됩니다.

 

 

 

이렇게 구해진 오른쪽의 행렬이 역행렬입니다.

 

 

계산 과정을 상세하게 보여 주기 위해서 하나하나 써서 그렇지 연립 방정식의 가감법 혹은 소거법과 매우 비슷합니다.

 

실제 해보시면 굉장히 빠른 속도로 역행렬을 구하는 것이 가능합니다.

 

 

 

한번 생각해 보세요 연립 방정식을

 

 

 

 

 

이런 연립 방정식 못 푸시는 분은 없을 것입니다. 소거법이나 가감법으로 다들 풀수 있죠

위 연립 방정식 못푸는 사람 없을 것이라 생각합니다.

 

마찬가지 방법으로 가우스 소거법으로 역행렬을 구하는 것입니다.  과정을 풀어쓰다보니 길게 느껴지는 거지 직접 손으로 계산하면 무조건 1분 이내로 끝낼수 있습니다.

 

 

이러한 행렬을 다룰 시, Rank라는 개념이 존재합니다. 행렬식의 성질에서 각 행이나 열을 덧셈이나 뺄셈을 해도 행렬식 값은 유지되는 것이 있었습니다. 이때 각 행이나 열이 몇개나 독립인지를 나타내는 것이 Rank입니다.

 

예를 들어서 

위와 같은 행렬은 1행과 나머지 행이 모두 같습니다. 즉 위 행렬에서 독립된 행은 1개 이죠

 

이와 같이 만들 수 있기 때문에 위 A행렬은 Rank값이 1입니다.

 

이런 행렬은 각 행이 서로 독립입니다. 각 행을 서로 더하거나 빼는 걸로 인해서 다른 행을 없앨 수 가 없죠. 이때는 Rank값이 3이 됩니다. 생각보다 쉬운 개념입니다.

이와 같은 행렬은 Rank값이 어떻게 될까요?? 3행이 1행과 2행의 합이므로 3행은 독립이 아닙니다. 따라서 독립된 행이 2이므로 Rank B = 2가 되겠죠..

 

이와 같이 독립된 행,열의 갯수가 Rank값이 되는데 앞서 이야기한 transpose와 연관지어서 아래의 특성을 가집니다.

 

이런 rank값을 가지고 연립방정식의 해의 존재 여부를 알수 있습니다. 예를 들어서 아래와 같은 연립 방정식이 존재한다고 해봅시다.

물론 해가 존재하도록 만든 연립방정식이지만, 위 행령은 아래와 같이 간단히 표현이 가능합니다.

 

각 행이 0이 되는 행이 없으므로 Rank값은 그대로 3입니다. 이런 방법을 통해서 아래의 관계에 따라 해의 존재 여부를 파악할 수 있습니다

첫번째 경우는 위에서 제가 예를 든 경우입니다. 이 경우 해가 존재하는 형태로 자명해, 무수히 많은 해가 나올수 있습니다.

 

2번째 경우는 해가 없는, 즉 해가 존재하지 않는 경우입니다. 바로 다음장에서 다룰 고유치와 연관지으면 rank값은 0이 아닌 고유치의 개수입니다. 

 

이제 다음 장에서 고유치 및 고유백터에 대해 알아보겠습니다